¿Existe algo totalmente impredecible en la Naturaleza?

Antonio Acín (ICFO/ICREA, Barcelona, ​​España) y varios colegas responden a esta pregunta en un artículo en Nature Communications que presenta un protocolo cuántico para amplificar la aleatoriedad de los eventos naturales que sean aleatorios para hacerlos completamente aleatorios. El artículo no demuestra que estos eventos existan en la Naturaleza, pero introduce la siguiente dicotomía: o bien nuestro universo es completamente determinista, o bien existen eventos naturales que son totalmente aleatorios. Todo el mundo sabe que la física clásica es totalmente determinista (aunque el caos determinista limita su predictibilidad) y que la física cuántica permite lo aleatorio, aunque ello no implica la existencia de cualquier forma de aleatoriedad en la Naturaleza. El problema de distinguir entre (pseudo)aleatoriedad y aleatoriedad completa puede parecer de interés sólo para los filósofos, pero también es importante desde un punto de vista práctico, pues los bits aleatorios son útiles en muchas aplicaciones (protocolos criptográficos, juegos de azar o simulación numérica de sistemas físicos y biológicos). El artículo técnico es Rodrigo Gallego et al., «Full randomness from arbitrarily deterministic events,» Nature Communications 4: 2654, 30 Oct 2013 (arXiv:1210.6514 [quant-ph]).

Conferencia #Quantum13: El timo del ordenador cuántico comercial

Mi charla de 10 minutos en Passion for Knowledge – Naukas Quantum 13, impartida el miércoles 2 de octubre en San Sebastián/Donostia discuto los fundamentos de la computación cuántica y trato de explicar por qué el llamado “ordenador cuántico comercial” de la compañía D-Wave Systems no es un ordenador realmente cuántico. En 10 minutos no hay mucho tiempo para presentar los detalles técnicos, pero espero que te guste la charla. Tienes más detalles en «Por qué el ordenador “cuántico” D-Wave Two no es cuántico,» 27 Ago 2013; «Nuevo algoritmo de corrección de errores en recocido cuántico,» 02 Ago 2013; «Por primera vez en la historia se vende un ordenador cuántico “D-Wave One”,» 6 Jun 2011; y otras más.

El tiempo es lo que miden los relojes

Parece obvio, pero el tiempo es lo que miden los relojes; si no hay ningún reloj, no se puede medir el tiempo. La ecuación de Wheeler–De Witt para la función de onda cuántica del universo no depende del tiempo, pues no existe ningún reloj «fuera» del universo. Don N. Page y William K. Wootters en 1983 propusieron un modelo análogo a esta ecuación, el estado estacionario de un sistema cuántico que está formado por el entrelazamiento de dos subsistemas que evolucionan en el tiempo. Uno de los subsistemas se puede interpretar como «reloj» que permite definir una «flecha de tiempo» para medir la evolución en dicho «tiempo» del otro subsistema; sin embargo, el sistema completo es estacionario y no evoluciona en el tiempo. Ekaterina Moreva (INRIM, Turín, Italia) y sus colegas acaban de publicar en ArXiv una realización experimental de esta idea utilizando como sistema dos fotones entrelazados (la implementación más simple posible de la idea de Page y Wootters). El artículo técnico es Ekaterina Moreva, Giorgio Brida, Marco Gramegna, Vittorio Giovannetti, Lorenzo Maccone, Marco Genovese, «Time from quantum entanglement: an experimental illustration,» arXiv:1310.4691 [quant-ph], 17 Oct 2013, que implementa la idea de Don N. Page, William K. Wootters, «Evolution without evolution: Dynamics described by stationary observables,» Phys. Rev. D 27: 2885–2892, 1983.

Algunos medios han afirmado que se ha demostrado que el tiempo es emergente, pero en realidad sólo se ha confirmado que para medir el tiempo es necesario un reloj. Repito, parece algo obvio, pero mucha gente no lo tiene claro. El tema de los relojes en mecánica cuántica es muy interesante y el nuevo artículo aporta poco a lo ya conocido, lo que no quita que sea curioso y merezca aparecer reseñado en este blog. ¿Transcurre el tiempo cuando no hay ningún reloj que lo mida? Esta cuestión es filosófica, la física sólo estudia lo que se puede medir. A los interesados en más detalles les recomiendo leer alguno de los muchos artículos sobre la naturaleza del tiempo y su relación con los relojes, por ejemplo, Iñigo L. Egusquiza, Luis J. Garay, José M. Raya, «Quantum evolution according to real clocks,» Phys. Rev. A 59: 3236–3240, 1999.

Lo que une el «amor cuántico» no lo separa una multitud

Una pareja de novios caminando entre una multitud tiene grandes problemas para no separarse. No tendrían ningún problema si fueran dos excitaciones cuánticas (como un par de fotones o de magnones) y la multitud fuera los átomos de un cristal que se comportase como un medio no lineal. Se publican dos artículos en Nature que lo demuestran de forma experimental. Fukuhara et al. han logrado propagar una pareja de magnones (las excitaciones cuánticas que propagan la energía en los imanes) y Firstenberg et al. una pareja de fotones; en ambos casos la interacción que liga los cuantos de la pareja es mediada por los átomos del medio. La pareja de cuantos se mueven al unísono y para controlar su movimiento basta con que una fuente externa actúe sobre uno de ellos, lo que tiene interesantes aplicaciones en el procesado cuántico de información y en su transferencia. Nos lo cuenta Sougato Bose, «Condensed-matter physics: Quantum togetherness,» Nature, AOP 25 Sep 2013, que se hace eco de los artículos técnicos Takeshi Fukuhara, Peter Schauß, Manuel Endres, Sebastian Hild, Marc Cheneau, Immanuel Bloch, Christian Gross, «Microscopic observation of magnon bound states and their dynamics,» Nature, AOP 25 Sep 2013, y Ofer Firstenberg, Thibault Peyronel, Qi-Yu Liang, Alexey V. Gorshkov, Mikhail D. Lukin, Vladan Vuletić, «Attractive photons in a quantum nonlinear médium,» Nature, AOP 25 Sep 2013.

Francis en Trending Ciencia: Logran parar pulsos de luz durante un minuto

Ya puedes escuchar mi nuevo podcast para Trending Ciencia siguiendo este enlace. Como siempre, una transcripción, enlaces a los artículos técnicos y algunas imágenes.

He elegido como tema una noticia que Nuño Domínguez, periodista científico de esMateria.com, ha titulado como «Récord mundial: Científicos alemanes detienen la luz durante un minuto.» Nos cuenta que «en el laboratorio de física cuántica que dirige Thomas Halfmann (…) en la Universidad Técnica de Darmstadt, Alemania (…) [han paralizado] un rayo de luz durante un minuto: todo un récord mundial que casi multiplica por cuatro el anterior. El avance técnico es un importante paso hacia (…) una especie de internet [imposible de hackear] que funcione con luz y en el que los mensajes vayan [cifrados] usando fotones. Cualquier intento de interferir en esos fotones destruiría la clave o el mensaje que transportan, lo que hace que la clave sea teóricamente inexpugnable. Pero para poder enviar mensajes con fotones [hay que] construir (…) una memoria informática que los guarde [todo el tiempo que sea necesario].»

Nuño Domínguez nos cuenta esMateria.com que «la técnica de Halfmann consiste en disparar un primer rayo láser de control a un cristal opaco, lo que lo vuelve transparente. Después se dispara un segundo láser, que lleva un mensaje, en este caso una imagen. En ese momento se apaga el primer rayo láser y el mensaje queda encerrado en el cristal. Aplicando campos magnéticos Halfmann logra que los átomos del cristal retengan la luz durante un tiempo récord, [sesenta segundos], un minuto. Después se enciende el primer láser, el cristal vuelve a tornarse transparente y la luz congelada en el tiempo vuelve a correr, transmitiendo su mensaje. Por ahora no han llegado al régimen de un solo fotón que se necesita para las memorias cuánticas.»

Algunos comentarios en Twitter me han llamado la atención. Unos por creer que se ha logrado parar los fotones individuales (algo obviamente imposible por definición de fotón). Otros por creer que se ha logrado a alta temperatura, mal interpretando la frase de Nuño Domínguez en esMateria.com: «Este mismo año, otro equipo de EEUU logró el récord [anterior] al retener la luz durante 16 segundos dentro de una nube de gas a unos 273 grados bajo cero, algo que ahora ha quedado totalmente pulverizado con la Transparencia Inducida Electromagnéticamente (EIT, en inglés) usada por Halfmann.» El nuevo récord de 60 segundos se ha logrado con el cristal enfriado a 4 Kelvin, es decir, a 269 grados bajo cero. De hecho, poder aplicar la nueva técnica a pocos fotones, o incluso a un sólo fotón, con seguridad requerirá bajar la temperatura a unos micro- o nano-Kelvin. Permíteme una discusión sobre el nuevo resultado técnico de Halfmann y sus colegas, cuyo mayor interés es que se ha utilizado un cristal, un dispositivo de estado sólido, en lugar de un gas de átomos ultrafríos o un condensado de Bose-Einstein.

ER=EPR, la nueva conjetura de Maldacena y Susskind

La ecuación ER=EPR hace referencia a dos ideas que Albert Einstein publicó en 1935, los puentes de Einstein−Rosen y el entrelazamiento cuántico de Einstein−Podolsky−Rosen. El artículo EPR fue una «bella durmiente de la ciencia» y ER va camino de serlo. La conjetura ER=EPR afirma que hay un puente de Einstein-Rosen (un tipo de agujero de gusano inestable entre dos agujeros negros) asociado a cada pareja de estados cuánticos entrelazados (estados EPR). Esta idea no es nueva, pero ha sido rescatada por el famoso físico argentino Juan Maldacena, autor del artículo más citado de la historia en SPIRES-HEP (el de la correspondencia AdS/CFT o gravedad/gauge). Maldacena y Susskind han aplicado esta idea para resolver el problema de los «firewalls» de Polchinski et al. (AMPS) en el horizonte de sucesos. Si eres físico y no has leído aún el artículo de Juan Maldacena, Leonard Susskind, «Cool horizons for entangled black holes,» arXiv:1306.0533, Subm. 3 Jun 2013, ¿a qué estas esperando? Si es muy técnico para tí, te recomiendo leer John Preskill, «Entanglement = Wormholes,» Quantum Frontiers, Jun 7, 2013. Otra visión diferente la ofrece Lubos Motl, «Maldacena, Susskind: any entanglement is a wormhole of a sort,» The Reference Frame, June 8, 2013, y «Papers on the ER-EPR correspondence,» TRF, July 9, 2013. Algo mucho más ligero en Jacob Aron, «Wormhole entanglement solves black hole paradox,» NewScientist, 20 Jun 2013.

Fabrican el espejo perfecto utilizando un cristal fotónico

Se publica en Nature la fabricación del primer espejo perfecto gracias a un cristal fotónico de nitruro de silicio sobre un sustrato de dióxido de silicio, un espejo que refleja toda la luz incidente, sin absorber nada de luz; la luz debe incidir con un ángulo concreto desde un líquido con el mismo índice de refracción que el dióxido de silicio (como muestra la figura). Un cristal fotónico es un material microestructurado que presenta una serie de pequeños agujeros con un tamaño menor que la longitud de onda de la luz incidente. El cristal fotónico actúa como un sólido y presenta una serie de bandas prohibidas para la luz (como un sólido las presenta para los electrones). Los cristales fotónicos permiten nuevos modos de guiado de la luz, permitiendo que la luz se curve en una esquina sin pérdidas y otros fenómenos similares. ¿Por qué funciona el cristal fotónico como espejo perfecto? Según los autores aparece un fenómeno similar a la interferencia destructiva que se observa en algunos sistemas cuánticos; el acoplo entre los modos evanescentes a ambos lados del cristal fotónico presenta una resonancia que hace que se desvanezcan. En física cuántica a este fenómeno se le llamada degeneración accidental y fue propuesto en 1929 por John von Neumann y Eugene Wigner; la ecuación de Schrödinger permite que en un pozo de potencial haya estados de electrones atrapados con la misma energía que un electrón libre (infinitamente alejado del potencial). ¿Para qué puede servir? Quizás para atrapar luz dentro de una cavidad óptica con espejos perfectos a ambos lados. Nos lo cuenta A. Douglas Stone, «Optical physics: Trapping the light fantastic,» Nature 499: 159–160, 11 Jul 2013, quien se hace eco del artículo técnico de Chia Wei Hsu et al., «Observation of trapped light within the radiation continuum,» Nature 499: 188–191, 11 Jul 2013. Por cierto, uno de los autores, John D. Joannopoulos (MIT) es firme candidato al Premio Nobel de Física por los cristales fotónicos desde hace más de una década.

Francis en Trending Ciencia: El problema del colapso de la función de onda

Ya puedes disfrutar de mi nuevo podcast sobre física para Trending Ciencia. Sigue este enlace y como siempre, disfruta de la transcripción del audio, algunas imágenes y enlaces a los artículos técnicos.

Este año se cumplen 100 años del modelo cuántico de Bohr para el átomo. Por ello hoy hablo de mecánica cuántica y de uno de los debates más importantes sobre la interpretación de la mecánica cuántica. El problema de la medida en mecánica cuántica y la elegante solución que han ofrecido Armen E. Allahverdyan, Roger Balian, Theo M. Nieuwenhuizen, «Understanding quantum measurement from the solution of dynamical models,» Physics Reports 525: 1-166, April 2013 [arXiv:1107.2138]. Según estos investigadores la evolución unitaria conjunta del sistema medido y del aparato de medida gracias a la ecuación de Schrödinger explica el supuesto colapso de la función de onda gracias a que el aparato de medida tiene suficientes grados de libertad como para evolucionar de forma irreversible hacia el registro del resultado de la medida. La solución más sencilla a un problema suele ser demostrar que no existe tal problema.

Francis en Trending Ciencia: El principio de incertidumbre de Heisenberg

Ya puedes disfrutar de mi nuevo Podcast sobre Física para Trending Ciencia siguiendo este enlace. Como siempre una transcripción del audio, figuras y referencias a artículos y fuentes para profundizar.

Ha llegado a portada en el portal de noticias Menéame una cuyo titular es «Científicos vieneses demuestran empíricamente la violación del Principio de Indeterminación de Heisenberg.» La noticia enlaza un artículo técnico aparecido en ArXiv el 30 de mayo, arXiv:1305.7251, titulado «Violation of Heisenberg’s error-disturbance uncertainty relation in neutron spin measurements,» [Violación de la relación de incertidumbre de Heisenberg tipo error-perturbación usando medidas del espín del neutrón], firmado por Georg Sulyok, de la Universidad Técnica de Viena, y varios colegas. La entradilla en Menéame traduce la última frase del artículo, en la sección de conclusiones: «Conclusión: Así pues, nuestros resultados dan una demostración experimental de que la forma generalizada de la relación error-perturbación de Heisenberg tiene que ser abandonada.» Esta noticia en portada de Menéame ha generado mucho revuelo en Twitter y en varias ocasiones he tenido que aclarar que no se ha demostrado que el sacrosanto principio de indeterminación de Heisenberg es falso, más bien todo lo contrario, se ha reforzado su validez. El titular se puede tachar de sensacionalista y la entradilla parece indicar que el meneante de la noticia no se ha leído en detalle la introducción del artículo técnico. Permíteme una aclaración en este podcast para Trending Ciencia.

Antes de nada, en mi misma línea, quiero destacar que también ha sido portada en Menéame una entrada mi amigo cordobés Enrique F. Borja, físico responsable del blog Cuentos Cuánticos, quien ha aclarado esta cuestión en su nuevo blog «Es Extraño…» en el portal de blogs de la revista Investigación y Ciencia. Su artículo titulando «Heisenberg todavía está tranquilo,» aclara lo que significa el principio de indeterminación de Heisenberg, en qué consiste el nuevo resultado y cómo no viola dicho principio, sino todo lo contrario, lo apoya de forma irrefutable.

Yo ya lo dije en Twitter «La formulación original del principio de incertidumbre de Heisenberg sólo es válida para pulsos gaussianos. Verificar que [dicha formulación] es violada para pulsos generales no es [ninguna] novedad. Y no afecta a la validez general del principio. Lo que se estudia [en el nuevo artículo] es la validez de la formulación original de Heisenberg de 1927, que no es la viene en los libros de texto, y que se sabe desde pocos meses después de ser publicada que debe ser modificada ligeramente.» Permíteme aclare estos puntos, porque quizás muchos de los oyentes no me siguen en Twitter y no se enteraron de mis comentarios.

Werner Heisenberg (1901-1976) fue uno de los padres de la mecánica cuántica y formuló en 1925 lo que ahora se conoce como mecánica cuántica matricial, en la que las magnitudes físicas, como la posición y la velocidad (o el momento lineal), se describen mediante matrices que no conmutan entre sí. En 1927, Heisenberg escribe el artículo en el que enuncia su famoso principio de indeterminación que afirma que «hay parejas de magnitudes físicas que no están determinadas con total precisión de forma simultánea.» Estas parejas de magnitudes físicas son las representadas por operadores o matrices que no conmutan entre sí. Sin embargo, en la formulación matemático original, Heisenberg formuló su principio utilizando un ejemplo particular, la medida de la posición y el momento lineal de un electrón en el estado fundamental de un átomo utilizando fotones. Heisenberg presenta su famosa desigualdad para la influencia del error cuadrático medio en las medidas experimentales de la posición en la incertidumbre del momento lineal, también medida como error cuadrático medio. Dicha formulación original del principio que le llevó a recibir el Premio Nobel de Física en 1932, no corresponde a lo que todos los estudiantes de física estudian durante la carrera ya que asume que el error en las medidas experimentales está equidistribuido (es decir, sigue una distribución gaussiana o campana de Gauss). Muy pocos libros de texto de física cuántica, salvo los que presentan la historia original de esta teoría, describe la formulación del principio de Heisenberg utilizando el error cuadrático medio en las medidas de posición y momento lineal, pues dicha expresión matemática tiene una validez limitada, ya que en el caso general la función de onda no es un paquete gaussiano, es decir, no implica una distribución de probabilidad de tipo campana de Gauss.

W. Heisenberg, «Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik,» Zeitschrift für Physik 43: 172-198, 1927 [traducción al inglés «The actual content of quantum theoretical kinematics and dynamics,» NASA TM-77379, 1983].

La formulación del principio de incertidumbre de Heisenberg que todos los físicos estudiamos en los libros de texto es la que presentó el físico norteamericano Earl H. Kennard en 1927, pocos meses después de la publicación del artículo original de Heisenberg. Esta formulación está basada en la dispersión típica de los operadores de posición y momento lineal. De hecho, en la mayoría de los libros de texto de mecánica cuántica el principio de Heisenberg se presenta en su formulación general publicada en 1929 por el físico norteamericano Howard P. Robertson, que relaciona la dispersión típica de dos observables que no conmutan con su conmutador. Ni Kennard ni Robertson tienen su nombre asociado al de Heisenberg, aunque sus formulaciones matemáticas son más correctas que la de Heisenberg pues son válidas para una función de onda general; pero ello no quita que la formulación física del principio de incertidumbre de Heisenberg sea la correcta. Esto algo muy habitual en los trabajos pioneros de física; las ideas físicas son correctas pero la formulación matemática original tiene una validez limitada.

E. H. Kennard, «Zur Quantenmechanik einfacher Bewegungstypen,» Zeitschrift für Physik 44: 326-352, 1927; H. P. Robertson, «The Uncertainty Principle,» Phys. Rev. 34: 163-164, 1929.

¿Se puede corregir la formulación original de Heisenberg para paquetes gaussianos y obtener una formulación completamente general siguiendo su línea de razonamiento? Por supuesto, aunque quizás sorprenda a muchos oyentes que esta cuestión ha sido poco estudiada. Aunque desde pocos meses después de la formulación original de Heisenberg en 1927 se sabe que su formulación original basada en el error cuadrático medio no es válida en el caso general y ha de ser corregida, se considera que el valor de esta corrección tiene interés sólo para los físicos aficionados a la historia de la física. A mi pesar, la mayoría de los físicos no están interesados en la historia de la mecánica cuántica e ignoran este tipo de cuestiones de importancia menor, por no decir de importancia nula. Sólo a los físicos que somos apasionados a la historia de nuestra ciencia nos interesan este tipo de detalles históricos.

El físico japonés Masanao Ozawa, de la Universidad de Tohoku, reformuló en el año 2002 las ideas originales de Heisenberg y descubrió cómo corregir su formulación original utilizando errores cuadráticos medios para que sea aplicable a funciones de onda generales. Por supuesto, su formulación incluye dos términos adicionales que dan cuenta de la contribución de la desviación típica de los operadores involucrados. Sin entrar en detalles técnicos, la formulación de Ozawa del principio de incertidumbre de Heisenberg pasó sin pena ni gloria, hasta que ahora el propio Masanao Ozawa ha visitado Viena para solicitar a sus colegas de la Universidad Técnica de Viena que verifiquen de forma experimental su formulación del principio de incertidumbre. De hecho, el artículo técnico cuyo primer autor es Georg Sulyok incluye a Ozawa como quinto autor.

Masanao Ozawa, «Physical content of Heisenberg’s uncertainty relation: Limitation and reformulation,» Phys. Lett. A 318: 21-29, 2003 [arXiv:quant-ph/0210044].

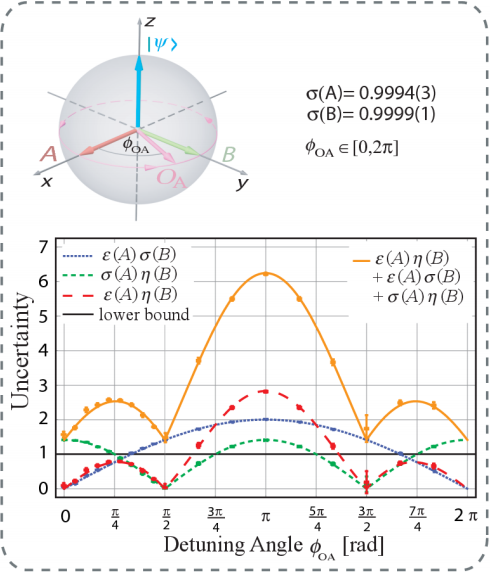
No quiero entrar en los detalles técnicos del experimento realizado por Sulyok y sus colegas, que utiliza dos componentes del espín de un neutrón en lugar de la posición y el momento lineal de un electrón en un átomo. Lo más importante en dicho experimento es que se han medido de forma separada los errores cuadráticos medios de ambas componentes del espín y las desviaciones típicas de los correspondientes operadores cuánticos, demostrándose que el principio de incertidumbre de Heisenberg en su formulación convencional, con desviaciones típicas se cumple, pero que también se cumple en la formulación de Ozawa. Como la contribución de los términos introducidos por Ozawa en la formulación original de Heinsenberg ha sido demostrada con precisión, el artículo técnico proclama que se ha demostrado por primera vez de forma empírica que la formulación original de Heisenberg para los errores cuadráticos medios es incorrecta. Ninguna novedad para los físicos, que ya lo sabían desde que en 1927 se publicó el artículo de Kennard.

Georg Sulyok, Stephan Sponar, Jacqueline Erhart, Gerald Badurek, Masanao Ozawa, Yuji Hasegawa, «Violation of Heisenberg’s error-disturbance uncertainty relation in neutron spin measurements,» arXiv:1305.7251, 30 May 2013. También recomiendo consultar Jacqueline Erhart, Stephan Sponar, Georg Sulyok, Gerald Badurek, Masanao Ozawa, Yuji Hasegawa, «Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin-measurements,» arXiv:1201.1833, 9 Jan 2012.

El físico japonés Ozawa ya tiene su pequeño momento de gloria, que será olvidado rápidamente por todo el mundo. Pues ya se sabe que no es noticia que un perro muerda a una persona, sino que una persona muerda a un perro. Y tampoco es noticia verificar de forma experimental que está mal lo que todo el mundo sabía que está mal. Eso sí, para mí es un artículo técnico muy interesante que recomiendo a todos los profesores de física cuántica. Pues recordar la historia de nuestra ciencia es una de las grandes asignaturas pendientes de la educación en la actualidad.

Coda final. Si no lo has hecho ya, puedes disfrutar de mi nuevo Podcast sobre Física para Trending Ciencia siguiendo este enlace.

PS: Por cierto, acaba de aparecer en ArXiv una nueva reformulación de la versión original de la relación de incertidumbre de Heisenberg de 1927 en Paul Busch, Pekka Lahti, Reinhard F. Werner, «Proof of Heisenberg’s error-disturbance relation,» arXiv:1306.1565, 6 Jun 2013. Esta nueva reformulación se diferencia de la de Osawa en que no utiliza la desviación típica de forma explícita y, por tanto, sigue de forma más fiel el espíritu de la formulación original de Heisenberg.

PS (28 jun 2013): Recomiendo leer el artículo de Ron Cowen, «Proof mooted for quantum uncertainty. Study confirms principle’s limits on measurement accuracy,» Nature 498: 419–420, 27 Jun 2013.

Francis en Trending Ciencia: Visualizan el entrelazamiento cuántico entre dos fotones

Ya puedes disfrutar de mi nuevo podcast para Trending Ciencia siguiendo este enlace. Como siempre, una transcripción del audio.

Anton Zeilinger, el famoso físico austriaco que es eterno candidato al Premio Nobel de Física, y sus colegas en la Universidad de Viena, ha preparado un vídeo de youtube en el que visualiza el entrelazamiento cuántico en polarización entre dos fotones. El vídeo es espectacular y no te lo deberías perder. En mi blog tienes el enlace. Dicho vídeo se ha preparado como información suplementaria a su artículo de acceso gratuito «Real-Time Imaging of Quantum Entanglement» («imagen en tiempo real del entrelazamiento cuántico»), cuyos autores son Robert Fickler, Mario Krenn, Radek Lapkiewicz, Sven Ramelow y Anton Zeilinger, publicado en la revista del grupo Nature Scientific Reports el pasado 29 de Mayo de 2013. 

Robert Fickler, Mario Krenn, Radek Lapkiewicz, Sven Ramelow & Anton Zeilinger, «Real-Time Imaging of Quantum Entanglement,» Scientific Reports 3: 1914, 29 May 2013. Más información en «Sean Carroll, «The Universe on a StratocasterNew Video Project,» S = k log W, May 29, 2013.

La polarización es una propiedad de la luz cuyo origen cuántico es el hecho de que el campo electromagnético es un campo con dos campos componentes independientes. Un sólo fotón tiene una polarización bien definida que está definida por un ángulo. En un laboratorio de óptica cuántica podemos generar un fotón con una polarización dada; por ejemplo, a cero grados o polarización horizontal |H>, a 90 grados o polarización vertical |V>, o incluso a cualquier ángulo intermedio; en este último caso, si escribimos el estado del fotón como coseno de alfa por el estado horizontal más seno de alfa por el estado vertical (cos(α) |H> + sin(α) |V>) encontramos que al medir la polarización del fotón será horizontal |H> con una probabilidad de cos²(α) y será vertical |V> con una probabilidad de sin²(α). En un laboratorio de óptica cuántica disponemos de detectores de polarización que podemos ajustar para medir polarización horizontal, vertical o en cualquier otro ángulo. Si un fotón en polarización horizontal incide en un detector ajustado a polarización vertical, la probabilida de de detectarlo será cero, si incide uno con polarización vertical será del 100% y si incide uno a 45 grados será del 50%.

En los laboratorios de óptica cuántica se dispone de generadores de pares fotones entrelazados en polarización, dispositivos capaces de generar dos fotones indistinguibles entre sí en los que uno está polarizado en horizontal y el otro en vertical. Como no sabemos cuál es el cuál es estado cuántico de los dos fotones es un estado de superposición de las dos posibilidades, que el primer fotón esté en horizontal y el segundo en vertical, y que el primer fotón esté en vertical y el segundo en horizontal, sea un estado entrelzadado |HV> + |VH>. No sabemos cuál es la polarización de cada uno de los fotones, lo único que sabemos es que ambas polarizaciones son complementarias entre sí. Al detectar uno de los fotones y obtener como resultado una polarización horizontal sabemos de inmediato que la polarización del otro fotón será vertical, incluso si dicho fotón se encuentra muy lejos.

Para visualizar el entrelazamiento cuántico, el físico austríaco Zeilinger y sus colegas en la Universidad de Viena han decidido grabar en vídeo los dos detectores de fotones, un detector de polarización diagonal, cuyo ángulo α se puede variar, sobre el que incide el primer fotón y un detector en polarización vertical sobre el que incide el segundo fotón. Estos detectores son pantallas CCD ultrarrápidas de alta sensibilidad. Cada vez que un fotón es detectado en una de estas pantallas CCD se observa un destello de luz. Cuando se graban en vídeo de forma continua los destellos de luz en ambos detectores lo que se observa es que los fotones inciden de forma aleatoria en cada detector y no hay ningún patrón visible. A veces hay un destello en un detector, a veces en el otro, y a veces en ambos. El resultado parece completamente aleatorio. Nada indica que la fuente de los fotones los hubiera entrelazado entre sí.

Para visualizar el entrelazamiento cuántico hay que hacer el siguiente truco. Grabar la imagen de vídeo con ambos detectores sólo cuando uno de ellos detecta un fotón. Zeilinger y sus colegas han elegido el detector diagonal a un cierto ángulo en la parte izquierda de la imagen  del vídeo y un detector horizontal en la parte derecha de la imagen. Cuando un fotón incide sobre el detector diagonal colocado a 45 grados, si dicho fotón es horizontal o vertical puede producirse un destello con un 50% de probabilidades. Si de la grabación del vídeo anterior quitamos los fotogramas en los que sólo uno de los detectores produce destello y dejamos sólo los fotogramas en los que ambos detectores producen destellos, en lugar de una imagen aleatoria se observa un patrón muy curioso en ambos lados de la imagen. En el detector diagonal se observan dos franjas verticales separadas por una región vacía y en el detector horizontal un aro circular con el centro vacío. Más aún, variando el ángulo del detector diagonal (o el ángulo de polarización de los fotones entrelazados) se observa como el patrón de dos franjas verticales se pone a rotar   acompañado del otro patrón. El vídeo es realmente espectacular.

El entrelazamiento cuántico es una de las consecuencias más importantes de la física cuántica y tiene múltiples aplicaciones. Yo destacaría su aplicación en la computación cuántica: el paralelismo cuántico consiste en aplicar un operador cuántico a un registro de bits cuánticos entrelazados; cada cubit puede tener dos estados posibles y el registro de n cubits puede tener 2 elevado a n estados posibles. Aplicar una operación cuántica a dicho registro de n cubits es equivalente a aplicar dicha operación a cada uno de los 2 elevado a n estados posibles, por lo que si se quisiera simular dicha operación con un ordenador clásico habría que utilizar 2 elevado a n operaciones clásicas. El entrelazamiento cuántico es el secreto del paralelismo cuántico y de la eficiencia de los ordenadores cuánticos a la hora de resolver ciertos problemas.

El nuevo vídeo de Zeilinger y sus colegas seguro que acabará formando parte de las ilustraciones multimedia de todos los cursos de física  cuántica, como ya forma parte de ella el vídeo Akira Tonomura y sus colaboradores de Hitachi en 1989 sobre el experimento de doble rendija.

Más información en «El experimento de la doble rendija de Hitachi o el experimento más bello de toda la física.»

Si no has escuchado aún el audio de mi podcast, sigue este enlace.