¿Cuántas moléculas de H2O se necesitan para formar agua líquida?

Nadie sabe la respuesta, pero parece evidente que debe ser un número finito de moléculas. Jeong-Hyuck Park (DAMTP, Univ. Cambridge, GB) ha calculado por ordenador, gracias a una analogía con un gas ideal de bosones, que en una caja cúbica se requieren 7.616 moléculas de agua y en un caja esférica 10.458. Conforme el número de moléculas en un gas a presión constante crece se produce una transición de fase que el autor considera que está asociada a la «emergencia» del concepto de agua. Para caracterizar una transición de fase entre dos fases se utiliza un diagrama que presenta la temperatura en función de la composición de ambas fases, la llamada descomposición espinodal; Park ha calculado el número de moléculas de agua para que aparezca un cambio brusco en la curva espinodal del sistema de bosones. El autor propone que este cambio es una característica genérica de las transiciones de fase líquido-gas, es decir, que la ebullición es un fenómeno emergente y puede ser calculada ab initio utilizando los principios básicos de la física estadística. Futuros estudios tendrán que refinar estos números y estudiar en detalle la dependencia con la forma del volumen que contiene el gas de bosones y las condiciones de contorno utilizadas (Dirichlet en este caso). El artículo técnico es Jeong-Hyuck Park, «How many is different? Answer from ideal Bose gas,» arXiv:1310.5580 [cond-mat.stat-mech], 21 Oct 2013. El artículo que realizó el cálculo es Jeong-Hyuck Park, Sang-Woo Kim, «Thermodynamic instability and first-order phase transition in an ideal Bose gas,» Phys. Rev. A 81: 063636, 2010.

Un motor térmico basado en átomos ultrafríos

El efecto termoeléctrico es la producción de una corriente eléctrica (transporte de electrones) gracias a una diferencia de temperatura (gradiente térmico). Un efecto similar es el transporte de átomos entre dos nubes de átomos ultrafríos, ambas con el mismo número de átomos, cuando una de ellas es calentada por un láser. La nube de átomos caliente se expande, reduciendo su densidad, por lo que uno espera un flujo de partículas del depósito más frío y más denso al más caliente y menos denso. Sin embargo, se observa el efecto contrario, las partículas fluyen de la nube de átomos más caliente a la más fría. El transporte de los átomos ocurre desde el depósito con un potencial químico menor al que tiene uno mayor, es decir, el sistema se comporta como un motor térmico de átomos ultrafríos. Este curioso experimento se publica en Science y podría tener aplicaciones en sistemas de refrigeración de circuitos nanoelectrónicos. El artículo técnico es Jean-Philippe Brantut et al., «A Thermoelectric Heat Engine with Ultracold Atoms,» Science, AOP, Oct 24, 2013 [DOI]; arXiv:1306.5754 [cond-mat.quant-gas].

Francis en ¡Eureka!: Nanocristales para ventanas inteligentes

Ayer se inició la nueva temporada de mi sección ¡Eureka! en La Rosa de los Vientos, Onda Cero. Puedes escuchar el audio siguiendo este enlace. Como siempre, una transcripción y algunos enlaces para profundizar.

Muchos jóvenes científicos españoles se ven obligados a emigrar en el mejor momento de sus carreras y están logrando grandes éxitos fuera de España. La noticia de hoy es sobre una joven catalana que emigró a EEUU. Anna Llordés realizó su tesis doctoral en nanocristales en el Instituto de Ciencia de Materiales de Barcelona, que pertenece al CSIC, y la defendió en el año 2010 en la Universidad Autónoma de Barcelona. Tras la tesis emigró a EEUU, como postdoc en el Laboratorio Nacional Lawrence Berkeley en California. Al final, desde mayo de 2013, está contratada allí como investigadora, pero mantiene colaboraciones con sus compañeros españoles en el campo de los nanocristales, como Jaume Gázquez. Ha sido noticia que su último artículo sobre la aplicación de los nanocristales a ventanas inteligentes ha llegado a portada de la prestigiosa revista Nature, quizás la más prestigiosa del mundo. Un logro que pocos españoles han conseguido.

Más información en «Nuevo material electrocromático para ventanas inteligentes,» 22 Ago 2013. El artículo técnico es Anna Llordés, Guillermo Garcia, Jaume Gazquez, Delia J. Milliron, “Tunable near-infrared and visible-light transmittance in nanocrystal-in-glass composites,” Nature 500: 323–326, 15 Aug 2013. Más información en español en «Ventanas inteligentes con nanocristales permiten regular luz y calor,» ALT1040, que incluye un vídeo promocional en inglés de la empresa.

Francis en Trending Ciencia: Nanotermómetros

Ya puedes escuchar mi nuevo podcast sobre Física para Trending Ciencia siguiendo este enlace. Como siempre una transcripción del audio, enlaces a los artículos técnicos y algunas imágenes.

Un artículo publicado el pasado 13 de junio en la revista Nature, entre cuyos autores se encuentran Juan Carlos Cuevas y Linda Angela Zotti, investigadores del Departamento de Física Teórica de la Materia Condensada de la Universidad Autónoma de Madrid (UAM). Junto a otros colegas de la Universidad de Michigan (EEUU) han estudiado la disipación de calor en nanodispositivos utilizando un dispositivo de medida que podemos bautizar sin rubor como nanotermómetro. El nuevo termómetro a escala nanométrica es una sonda en forma de punta, similar a la utilizada en un microscopio por efecto túnel, capaz de medir la cantidad de calor disipado en un nanocircuito formado por átomos y moléculas individuales. Estudiar la disipación de calor en los nanocircuitos tales como nanocables semiconductores, heteroestructuras semiconductoras, nanotubos de carbono, grafeno y muchos otros es fundamental para el futuro desarrollo de la nanoelectrónica. Por ello, el nuevo nanotermómetro es un avance realmente espectacular.

El artículo técnico es Woochul Lee et al., «Heat dissipation in atomic-scale junctions,» Nature 498: 209–212, 13 Jun 2013. Más información en español en UAM, «Esclarecen cómo se disipa el calor en dispositivos nanotecnológicos,» SINC, 12 jun 2013.

Supongo que ya sabrás que el trasporte de electricidad por un cable o por un circuito eléctrico viene acompañado del calentamiento del cable o del circuito. El transporte de carga eléctrica siempre lleva asociada la disipación de calor por efecto Joule, descubierto en 1841 por el físico inglés James Prescott Joule, uno de los padres de la Termodinámica. Este efecto describe el calentamiento de un conductor por el que pasa una corriente eléctrica. En nuestros hogares hay muchos dispositivos basados en el efecto Joule, como secadores de pelo, calentadores de agua, incluso las bombillas de filamento se calientan por este efecto. El origen del efecto Joule son las colisiones de los electrones contra los iones de la estructura cristalina del material que atraviesan a su paso. El calor es el movimiento de estos iones respecto a sus posiciones de equilibrio y como este movimiento es acelerado por la interacción con los electrones, el conductor se calienta.

Todos los circuitos electrónicos se calientan y por ello los ordenadores requieren aletas de disipación de calor, ventiladores y otros sistemas de refrigeración. En los dispositivos a escala nanométrica el calor se disipa mediante la excitación de fonones, el modelo cuántica de las vibraciones de la estructura cristalina del material. Los autores del nuevo artículo publicado en Nature, entre ellos el español Juan Carlos Cuevas de la Universidad Autónoma de Madrid, han desarrollado unos nanotermómetros están formados por un electrodo recubierto en su exterior por una capa de oro conectada a un termopar de oro-cromo mediante una película delgada (de unos 70 nanómetros) de nitruro de silicio. A partir de la corriente medida en el termopar se puede inferir la cantidad de calor transferido en la punta del nanotermómetro cuando ésta se acerca al nanodispositivo que se esté estudiando.

Si el microscopio de efecto túnel revolucionó nuestra visión del mundo en la nanoescala, el nuevo nanotermómetro promete revolucionar nuestra comprensión de la disipación de calor en átomos y moléculas. Más aún, también demuestra el buen estado de la nanotecnología y de las nanociencias en general en España.

Coda final. Si aún no has escuchado el audio de mi podcast sobre Física para Trending Ciencia sigue este enlace.

El coste enzimático de la eficiencia en el metabolismo energético

Todo el mundo sabe que el coste de una obra de teatro además del trabajo de los actores incluye a mucho personal entre bambalinas. El coste termodinámico de una ruta metabólica también incluye un coste entre bambalinas, el coste proteómico de la síntesis de sus enzimas. Nos lo recuerda un nuevo artículo en PNAS que estudia en procariotas la ruta metabólica de la glucólisis, la síntesis de energía (moléculas de ATP) oxidando glucosa. La ruta metabólica estándar para la glucólisis es la de Embden-Meyerhoff-Parnass (EMP), que contiene 10 reacciones enzimáticas y cuyo producto son dos moléculas de ATP. Sin embargo, hay otras rutas para la glucólisis en procariotas, siendo la más común la ruta de Entner-Doudoroff (ED), que produce una sola molécula de ATP, pero sólo tiene 6 reacciones enzimáticas. Avi Flamholz (Instituto Weizmann de Ciencia, Rehovot, Israel) y sus colegas afirman que la prevalencia de la ruta ED en procariotas es debido a que requiere menos enzimas (6 en lugar de 10); este resultado lo han obtenido tras un análisis termodinámico de la cinética química de estas rutas metabólicas que incluye el coste termodinámico de la producción de las enzimas (normalmente despreciado en este tipo de análisis). El nuevo estudio nos recuerda que las bambalinas también existen en el metabolismo celular. Nos lo cuentan Arion I. Stettner, Daniel Segrè, «The cost of efficiency in energy metabolism,» PNAS, AOP May 31, 2013, quienes se hacen eco del artículo técnico de Avi Flamholz et al., «Glycolytic strategy as a tradeoff between energy yield and protein cost,»PNAS, AOP Apr 29, 2013.

Francis en Trending Ciencia: La física cuántica de la fotosíntesis

Sigue este enlace si quieres escuchar mi nuevo podcast en Trending Ciencia, que contesta una pregunta/petición formulada por Ces. Como siempre una transcripción del audio.

He elegido como tema para mi nuevo podcast sobre física la respuesta a una pregunta que me ha hecho uno de los lectores de mi blog, Ces, sobre la fotosíntesis y la física cuántica. Ces ha leído que la tasa de conversión de fotones en electrones en la clorofila alcanza el 90% gracias a la física cuántica. En realidad se trata de un mito. Igual que es falso que sólo usemos el 10% de nuestro cerebro, también es falso que la fotosíntesis tenga una eficiencia de más del 90%. La eficiencia máxima de la fotosíntesis como proceso bioquímico que produce biomasa a partir de radiación solar tiene una eficiencia máxima que ronda el 10%. Si sólo tenemos en cuenta los procesos que ocurren en las moléculas de clorofila, la eficiencia de la conversión de la energía de los fotones incidentes en el proceso de transferencia de electrones tiene una eficiencia que ronda el 50%. La eficiencia de más del 90% se refiere al proceso llamado «hopping» por el cual el fotón incidente en una molécula de clorofila produce una onda de tipo excitón que se mueve de forma sucesiva por varias moléculas de clorofila hasta alcanzar la molécula de clorofila «P» que realiza la transferencia de un electrón entre dos moléculas, una dadora de electrones y otra aceptora de electrones. Permíteme que explique todo esto en más detalle.

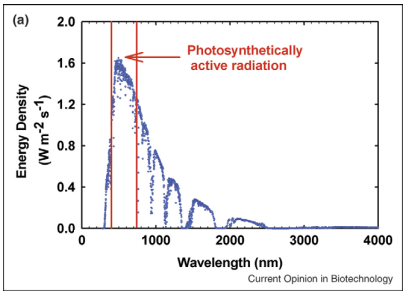
La luz del Sol que es activa para la fotosíntesis es la que se encuentra en la banda entre 400 y 700 nm; recuerda que la luz con 400 nm tiene color azul y que la luz con 700 nm tiene color rojo. Como la clorofila absorbe mal en el centro de esta banda, los colores verdes, las hojas de los árboles son verdes (en lugar de negras). Se estima que como mínimos el 5% (y en muchos casos hasta el 10%) de la luz solar en la banda de 400 a 700 nm que incide sobre las hojas de las plantas se refleja y por tanto no es útil para la fotosíntesis.

Los fotones que inciden sobre la molécula de clorofila provocan su transición energética a un estado excitado, cuya relajación posterior se utiliza para producir energía. Los fotones en la banda activa para la fotosíntesis, entre 400 y 700 nm, tienen una energía media por mol de fotones de 205 kJ (kilojulios). La energía necesaria para activar el sistema fotosintético fotosistema II (PSII) es la de un fotón con una longitud de onda de 680 nm, es decir, de unos 176 kJ/mol. Por otro lado, para el sistema fotosintético fotosistema I (PSI) es la energía de un fotón de 700 nm, es decir, 171 kJ/mol. Por tanto, en promedio, el 6,6% de la energía solar incidente se pierde en forma de calor durante la relajación de los estados excitados de la clorofila.

También se pierde energía en el ciclo de Calvin que sintetiza los carbohidratos a partir de CO2 y la energía capturada. En la fotosíntesis C3, el ciclo de Calvin consume tres moléculas de ATP (adenosín trifosfato) y dos de NADPH (nicotinamida-adenina-dinucleótido-fosfato) para asimilar una molécula de CO2 (dióxido de carbono) en un carbohidrato (glucosa) y generar la molécula necesaria para cerrar el ciclo. La síntesis de las tres moléculas de ATP requiere 12 protones (4 cada una) y las dos  moléculas de NADPH requiere absorber 8 fotones.  Todo esto por cada molécula de CO2 asimilada, proceso que requiere una energía de 1388 kJ por mol. Un sexto de un mol de glucosa, es decir, el carbono que le aporta la molécula de CO2, contiene unos 477 kJ. Por ello, en el ciclo de Calvin para la fotosíntesis C3 se pierde el 24,6% de la energía solar incidente. Sumando todos los efectos, en la fotosíntesis C3 la máxima cantidad de energía solar que se transforma en carbohidratos es del 12,6%.

Algo parecido ocurre en el caso de la fotosíntesis C4. Hay tres subtipos para el ciclo de Calvin en este caso. Sin entrar en detalles, se pierde el 28,7%  de la energía contenida en la radiación solar incidente. Por tanto la eficiencia máxima de conversión de energía en la fotosíntesis C4 se estima en un 8,5%. Pero no queda todo ahí, también hay pérdidas adicionales en la respiración que se produce en la mitocondria. Estas pérdidas dependen de varios factores. De nuevo sin entrar en detalles, se estima que entre el 30% y el 60% del a energía se pierde.

En resumen, tomando el porcentaje mínimo para todas las pérdidas de energía que hemos indicado, la eficiencia máxima de conversión de energía del Sol en biomasa en la fotosíntesis C3 es del 4,6% (de cada 1000 kJ de energía incidente sólo se transforma en biomasa 46 kJ) y en la fotosíntesis C4 es del 6,0% (de cada 1000 kJ de energía solar incidente sólo se transforma en biomasa 60 kJ).

Artículo técnico para los interesados en los detalles de estos cálculos: X.G. Zhu, S.P. Long, D.R. Ort, «What is the maximum efficiency with which photosynthesis can convert solar energy into biomass?,» Curr. Opin. Biotechnol. 19: 153-159, 2008.

Por supuesto, los oyentes me dirán que he tenido en cuenta demasiados efectos y que Ces en mi blog sólo estaba interesado en la eficiencia de la conversión de fotones en electrones en la clorofila. Permíteme considerar este proceso en detalle.

Un fotón incide sobre una «antena» molecular, un complejo proteíco formado por varias proteínas que contiene los pigmentos fotosintéticos (pongamos que sean moléculas de clorofila) y es absorbido excitando una molécula de clorofila, es decir, un electrón pasa desde un estado HOMO (siglas de orbital molecular ocupado de mayor energía) hasta un estado excitado no ocupado de mayor energía. Pocos picosegundos más tarde, esta molécula excitada decae, es decir, el electrón pasa desde el estado excitado a un estado LUMO (siglas de orbital molecular desocupado de menor energía) emitiendo un nuevo fotón. En este proceso la molécula vibra y pierde energía disipando calor. Obviando esta disipación térmica, la diferencia de energía entre los estados HOMO y LUMO debe corresponder a la energía del fotón absorbido por la molécula y a la energía del fotón emitido.

En las antenas moleculares fotosintéticas hay varias moléculas de clorofila que se excitan en secuencia a saltos (en inglés se habla de «hops» y al proceso se le llama «hopping» [también se utiliza el término «transferencian del excitón»]. Estos saltos acaban en una molécula de clorofila especial llamada clorofila «P» cuyo papel es la conversión del fotón en un electrón. La clorofila P está cerca de dos moléculas, una aceptora de electrones y otra dadora de electrones (DPA). Cuando la clorofila P se excita con un fotón (DP*A), decae en un proceso con dos etapas separadas: en la primera etapa transfiere un electrón a la molécula aceptora de electrones (DP+A-) y en la segunda etapa recibe un electrón de la molécula dadora de electrones (D+PA-), quedando en un estado no excitado tras este proceso.

La eficiencia energética de este proceso de conversión de energía la de un fotón en la transferencia de un electrón se puede calcular usando las leyes de la termodinámica. Podemos suponer que se trata de un ciclo de Carnot con un foco caliente, la energía de la molécula excitada, y un foco frío, la energía de la molécula en su estado fundamental. Asumiendo que la molécula de clorofila se comporta como una molécula en un gas, el cálculo resulta en una eficiencia máxima del 75%. Sin embargo, la clorofila in vivo no está en un gas y se encuentra acoplada a proteínas, lo que reduce la eficiencia a un valor entre el 57% y el 67%. Y en estos cálculos se ha omitido el trabajo requerido en las transiciones en las moléculas aceptora y dadora de electrones, lo que reduce la eficiencia de este ciclo de Carnot en como mínimo un 7% adicional.

En resumen, la eficiencia de la conversión de energía de un fotón a la de un electrón ronda el 60% en el mejor caso, siendo lo habitual que no supere el 50%. Pero entonces, ¿por qué comenta Ces en mi blog que ha leído que la eficiencia cuántica de la conversión de un fotón en un electrón en la fotosíntesis supera el 90%?

Más información sobre estos cálculos en Jérôme Lavergne, Pierre Joliot, «Thermodynamics of the Excited States of Photosynthesis,» BTOL-Bioenergetics, 2000 [pdf gratis].

La razón es sutil, pero sencilla. La eficiencia superior al 95% en la transferencia de energía en la fotosíntesis que mucha gente escribe en artículos de divulgación (yo mismo lo he escrito en mi blog en 2009) se refiere a la transferencia de los fotones entre moléculas de clorofila cercanas. El proceso que lleva los fotones desde la molécula de clorofila que ha capturado el fotón de la luz solar y la molécula de clorofila «P» que realiza la transferencia del electrón. El proceso de «hopping» tiene una eficiencia cercana al 95% gracias a la física cuántica, como se publicó en la revista Nature en el año 2007. Podemos decir que en este proceso de «hopping» se ejecuta un algoritmo cuántico de búsqueda que canaliza el fotón hasta la clorofila «P».

En mi blog puedes leer «La conexión entre la fotosíntesis y los algoritmos cuánticos,» 2009, y «Publicado en Nature: Biología cuántica y computación cuántica adiabática en la fotosíntesis a temperatura ambiente,» 2010.

En 2007, Gregory S. Engel (de la Universidad de California en Berkeley) y sus colegas estudiaron la fotosíntesis en la bacteria fototrópica verde del azufre (Chlorobium tepidum). Según su estudio experimental mediante espectroscopia bidimensional utilizando la transformada de Fourier, el proceso de «hopping» corresponde a la propagación coherente de una onda cuántica de tipo excitón que transfiere la energía del fotón capturado hasta el centro químico activo donde se realiza la transferencia del electrón [por eso al «hopping» también se le llama transferencian del excitón]. La onda cuántica se propaga por las moléculas de clorofila durante cientos de femtosegundos y se comporta como si “visitara” de forma simultánea varios caminos posibles y eligiera el óptimo para llegar al centro activo. Engel y sus colegas afirmaron en su artículo de 2007 que el proceso es análogo al algoritmo cuántico de Grover, capaz de buscar un elemento dado en un vector de n componentes desordenadas en un número de pasos igual a la raíz cuadrada de n (cuando un algoritmo clásico requiere mirar al menos todos los elementos, es decir, un tiempo proporcional a n). Aunque el estudio experimental publicado en el año 2007 se realizó con a baja temperatura, unos 77 Kelvin, los autores afirmaron que el mismo mecanismo debe ocurrir a temperatura ambiente.

Recomiendo leer a Roseanne J. Sension, “Biophysics: Quantum path to photosynthesis,” News and Views, Nature 446: 740-741, 12 April 2007. El artículo técnico original es Gregory S. Engel et al. “Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems,” Nature 446: 782-786, 12 April 2007.

De hecho, en el año 2010, se publicó en Nature otro artículo que comprobó dicho hipótesis, demostrando que el que dicho mecanismo también se da a temperatura ambiente. Elisabetta Collini (de la Universidad de Padua, Italia, aunque realizó la investigación trabajando en la Universidad de Toronto, Canadá) y sus colegas demostraron en un alga fotosintética que el mecanismo de «hopping» utiliza la coherencia cuántica incluso a temperatura ambiente. Pero repito, estos estudios, no implican que la eficiencia de la conversión de los fotones en electrones sea superior al 90%, como me preguntaba Ces en mi blog.

Recomiendo leer a Rienk van Grondelle, Vladimir I. Novoderezhkin, «Photosynthesis: Quantum design for a light trap,» Nature 463: 614-615, 4 Feb 2010. El artículo técnico es Elisabetta Collini et al., «Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature,» Nature 463: 644-647, 4 Feb 2010.

En resumen, espero haber contestado la pregunta de Ces de forma satisfactoria, aunque haya omitido muchos detalles técnicos. La fotosíntesis como proceso de conversión de energía solar en biomasa tiene una eficiencia máxima alrededor del 10%. El proceso fundamental que ocurre en la clorofila que permite la conversión de la energía de un fotón en la transferencia de un electrón tiene una eficiencia del orden del 50%. Y el proceso cuántico que tiene una eficiencia superior al 90% es el proceso de «hopping» por el que el fotón capturado en una molécula de clorofila recorre varias moléculas hasta llegar a la molécula de clorofila «P» que realiza la transferencia del electrón como tal.

Y esto es todo por hoy. Si te ha gustado la trancripción y quieres oír el podcast, sigue este enlace en Trending Ciencia.

Francis in Mapping Ignorance: Transferencia anómala de calor de lo frío a lo caliente

Te recomiendo leer mi última contribución al blog Mapping Ignorance, «Read it twice: Heat transfer from a cooler body to a hotter body,» May 16, 2013. El primer párrafo, en inglés, dice «Without any conflict with the second law of thermodynamics, heat can flow from a cooler but constantly heated body to another thermally connected and constantly hotter body. This anomalous heat transfer has been demonstrated in a two-phase liquid-vapor system composed of a Rayleigh–Bénard convection (RBC) cell filled one-half with normal liquid helium and one-half with helium vapor.» Seguir leyendo…

Mi contribución se basa en el artículo de Pavel Urban, David Schmoranzer, Pavel Hanzelka, Katepalli R. Sreenivasan, and Ladislav Skrbek, “Anomalous heat transport and condensation in convection of cryogenic helium,” PNAS 110(20): 8036-8039, May 14, 2013; además recomiendo consultar a Joseph J. Niemela, “Weather and anomalous heat flow occurring near absolute zero,” PNAS 110(20): 7969-7970, May 14, 2013.

El infrasonido del meteoro de Chelyabinsk y cómo se estimó su energía

Gracias a estos vídeos de youtube puedes oír el infrasonido producido por el meteoroide de Chelyabinsk, Montes Urales, Rusia, el pasado 15 de febrero. Esta grabación se obtuvo en la estación de la red CBTO (Comprehensive Test Ban Treaty Organisation) situada en la Antártida, a unos 15.000 km de distancia del evento. Grabaciones similares se obtuvieron en 17 estaciones de infrasonidos de la red CBTO. La entrada de un meteoroide en la atmósfera a velocidades hipersónicas y su posterior ablación producen una onda expansiva (onda de choque) que se propaga por la atmósfera y es audible a miles de kilómetros de distancia gracias a los infrasonidos. Estos sonidos no son audibles para el oído humano porque su frecuencias está en el rango de 0,001 a 20 Hz. Sin embargo, se puede modificar la frecuencia del sonido para hacerlo audible. Gracias a las medidas de la red de infrasonidos se puede estimar la posición (por triangulación), tamaño, masa, velocidad y energía liberada por el evento. Para ello se utilizan correlaciones experimentales obtenidas durante los últimos 60 años gracias a las pruebas de armas atómicas. En el caso del meteoro de Chelyabinsk se estimó que su diámetro fue de 17 metros, su masa de 10.000 toneladas y que liberó una energía equivalente a 500 kilotones de TNT.

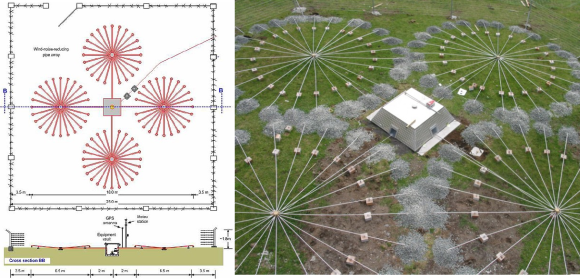
Estas dos figuras muestran resultados medidos por la estación de infrasonidos I31KZ, situada a unos 600 km al sur del hipercentro (fuente). La señal observada tiene frecuencias entre 0,004 Hz y 8 Hz.

Esta fotografía muestra la estación británica IS49 (Tristan da Cunha); el cuadrado tiene un lado de 25 metros y las rosetas radiales un diámetro de 6,5 metros (click para ampliar).

¿Cómo se estima la energía del suceso a partir de la señal de infrasonidos? Se utiliza una ley de potencias empírica obtenida tras el análisis de las pruebas de armamento nuclear realizadas durante la Guerra Fría (sobre todo en la década de los 1950). Estas fórmulas son las recomendadas por la AFTAC (United States Air Force Technical Applications Center) y aparecen en el libro de A. Le Pichon et al., «Infrasound Monitoring for Atmospheric Studies,» Springer, 2010. Se asume un modelo ideal de la onda de choque (sonic boom) dado por una onda tipo N. El periodo de esta onda en segundos permite determinar la energía W en kilotones de TNT. Hay modelos físico-matemáticos más detallados, pero requieren conocer un gran número de parámetros que no suelen estar disponibles.

La teoría más sencilla para describir el movimiento de un meteoro que no se fractura durante su ablación fue desarrollada por Öpik (1933, 1937) y Whipple (1938). En estas fórmulas, m es la masa del meteoro, ρ_m es su densidad, v es su velocidad, S es el área de su sección transversal, Γ es el coeficiente de fricción con la atmósfera,  ρ es la densidad de la atmósfera, Λ es el coeficiente de transferencia de calor (que mide la eficiencia de la transferencia al interior del meteoro del calor ganado por fricción), ξ es la energía de ablación del meteoroide (la energía necesaria para la ablación de una unidad de masa) y A es el llamado factor de cambio de forma. Estas fórmulas son aplicables a meteoroides con velocidades entre 11,2 km/s y 72,8 km/s, donde 11,2 km/s es la velocidad de escape de la Tierra y 72,8 km/s es la suma de la velocidad de escape del Sol a la distancia de la Tierra (42,5 km/s) más la velocidad orbital de nuestro planeta (30,3 km/s). En estas ecuaciones se ha despreciado el efecto de la gravedad en la trayectoria, pues el meteoroide atraviesa la atmósfera sólo durante unos pocos segundos, debido a su velocidad hipersónica. En el caso del meteoroide de Chelyabinsk estas fórmulas deberían ser corregidas con el efecto de la gravedad pues logró atravesar la atmósfera durante 32,5 segundos.

Los infrasonidos producidos por los meteoroides se llevan estudiando desde principios del siglo XX. Esta figura muestra una reconstrucción de la presión atmosférica sobre Europa el 30 de junio de 1908 cuando explotó a una altura de unos 10 km un meteoro sobre Tunguska en el centro de Siberia; se basa en las medidas de infrasonidos registradas en Washington DC que permitieron estimar que la energía liberada por este suceso fue equivalente a entre 10 y 12,5 megatones de TNT. Los infrasonidos permiten detectar el impacto de meteoros con un tamaño superior a pocos centímetros de diámetro. El registro observado permite estimar la masa del meteoroide, la velocidad de ingreso en la atmósfera y la energía total liberada por la desintegración del meteoro en la atmósfera.

La física detallada de procesos tan complicados como la ablación de un meteoro en la atmósfera está bien estudiada, pero en la práctica se utilizan modelos muy simplificados porque se ignoran gran número de los parámetros del meteoroide. Supongo que en los próximos meses se publicarán análisis detallados del suceso de Chelyabinsk. Ya os mantendré informados.

PS (27 feb 2013): Ya se han recogido gran número de fragmentos del meteoro de Chalyabinsk, aquí tenéis algunas fotografías.

PS (05 mar 2013): Recomiendo la lectura de T.A. Ens, P.G. Brown, W.N. Edwards, E.A. Silber, «Infrasound production by bolides: A global statistical study,» Journal of Atmospheric and Solar-Terrestrial Physics 80: 208–229, May 2012.

.

 

La polémica de los «cristales de tiempo»

En muchos sistemas físicos la rotura de una simetría conduce a un mínimo de energía estable. La energía se conserva en un sistema cuando es invariante ante traslaciones en el tiempo (si un experimento realizado hoy, ayer o mañana da el mismo resultado). Ya hablé en este blog de una idea de Frank Wilczek: que la rotura de la simetría ante traslaciones en el tiempo puede conducir a sistemas periódicos «eternos,» que no requieren aporte de energía, similares a móviles perpetuos, pero que Wilczek bautizó con el sugerente nombre de «cristales de tiempo.» Ya comenté que se publicaron tres artículos en Physical Review Letters sobre esta idea. Desde entonces se ha generado una buena polémica al respecto. Los retractores de la idea creen que los «móviles perpetuos,» aunque sean cuánticos, son imposibles. Los defensores se amparan en las sutilezas que diferencian los «cristales de tiempo» de los «móviles perpetuos,» apoyándose en el ejemplo de la superconductividad. Los superconductores, sistemas en los que fluye una corriente eléctrica sin resistencia, parecían imposibles, pero hoy en día los aceptamos sin más y se utilizan en muchos procesos industriales. ¿Algún día se construirá un «cristal de tiempo»? Nadie lo sabe, pero hay varias propuestas. Si alguna logra tener éxito, la polémica se resolverá reivindicando la genialidad de Wilczek (que parece no tener edad). Nos lo cuenta Piers Coleman, «Quantum physics: Time crystals,» Nature 493: 166-167, 10 January 2013. Los artículos técnicos en PRL son Frank Wilczek, “Quantum Time Crystals,” Phys. Rev. Lett. 109, 160401, October 15, 2012 [PDF gratis], Alfred Shapere, Frank Wilczek, “Classical Time Crystals,” Phys. Rev. Lett. 109: 160402, October 15, 2012 [PDF gratis], y Tongcang Li, Zhe-Xuan Gong, Zhang-Qi Yin, H. T. Quan, Xiaobo Yin, Peng Zhang, L.-M. Duan, Xiang Zhang, “Space-Time Crystals of Trapped Ions,” Phys. Rev. Lett. 109, 163001, October 15, 2012 [PDF gratis].

Francis en Naukas (con adenda): Qué significa que un gas cuántico tiene una temperatura negativa

Te recomiendo leer mi nuevo artículo en Naukas, «Qué significa que un gas cuántico tiene una temperatura negativa,» 04 enero 2013. «La temperatura absoluta de un gas ideal clásico mide la distribución de velocidades de las moléculas de dicho gas en un estado de equilibrio termodinámico. Para un gas clásico, una temperatura nula significa que todas las moléculas están en reposo. Por tanto, no tiene sentido físico una temperatura absoluta negativa aplicada a un gas clásico. (…) En mecánica estadística la temperatura tiene una interpretación probabilística. Gracias a la distribución de Boltzmann, la temperatura “mide” la probabilidad de que cada molécula de un gas ideal ocupe un estado con cierta energía. (…) Un sistema con temperatura absoluta negativa sería un sistema en equilibrio “invertido” en el que la probabilidad de ocupación de los estados crece de forma exponencial con la energía, es decir, los estados de menor energía están menos ocupados que los de mayor energía. Si la energía no tiene cota superior (energía máxima), es imposible que un sistema de este tipo esté en equilibrio. (…) Nada impide que se pueda lograr un sistema con temperatura absoluta negativa.  Para ello son necesarios dos requisitos.» Seguir leyendo en Naukas.com.

Ayer noche iba a escribir esta noticia para este blog, pero un poco más técnica que la que aparece en Naukas.com.