«El indomable Will Hunting» y los «árboles irreducibles con 10 vértices»

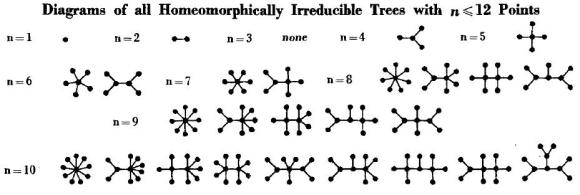
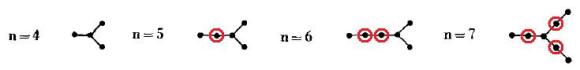Esta escena de la película «El indomable Will Hunting» (título original «Good Will Hunting») de 1997, dirigida por Gus Van Sant y protagonizada por Matt Damon y Ben Affleck (en la que también aparece Robin Williams) describe un problema matemático de la teoría de grafos: dibujar un sistema de representantes de las 10 clases de árboles con 10 vértices homeomórficamente irreducibles. La solución de este problema fue obtenida por Frank Harary, Geert Prins, «The number of homeomorphically irreducible trees, and other species,» Acta Mathematica 101: 141-162, 1959 [copia gratis]. La solución a este problema para árboles con hasta 10 vértices aparece en la siguiente figura, extraída de dicho artículo (en formato un poco más compacto).

En teoría de grafos, un árbol es un grafo en el que cada par de vértices está conectado sólo por un único camino. Una definición más técnica nos dice que un grafo simple no dirigido G con un número finito n de vértices es un árbol si cumple cualquiera de las siguientes condiciones (todas equivalentes entre sí): (1) es conexo y tiene n-1 aristas, o (2) es conexo y no tiene ciclos, o (3) tiene n-1 aristas y no tiene ciclos, o (4) existe una única trayectoria entre cada par de vértices [gracias Alberto por el comentario de más abajo]. El grado de un vértice es el número de aristas a las que está conectado. Una «hoja» es un vértice de grado 1. Un vértice interno es un vértice de grado mayor que 1. Un árbol es irreducible si no tiene vértices de grado 2.

En esta figura, el único árbol irreducible es el de n=4, ya que los de n=5, 6 y 7 vértices todos se pueden reducir a dicho árbol eliminando los vértices de grado 2 que están marcados con una circunferencia en color rojo.  Obtener todos los grafos con 10 vértices que son irreducibles no es difícil y cualquiera tanteando un poco puede hacerlo. Obviamente, lo más difícil es demostrar que no existe ningún otro.

¿Te atreves a dibujar todos los árboles irreducibles con n=11? No te pide que demuestres que tu lista es completa, sólo que lo intentes. No es un problema difícil (no creo que te requiera más de una hora de trabajo). Si lo haces te sentirás como Matt Damon (o como Will Hunting) Por supuesto, puedes chequear tu respuesta con el artículo original (que presenta los grafos irreducibles hasta n=12); también, hay programas de ordenador en la web que te permiten dibujarlos (si te gusta programar en Mathematica este problema es bonito para resolver por uno mismo sin buscar el notebook en la web). ¿Eres profesor de matemáticas? Por qué no le propones este problema a tus alumnos (resuelves el caso hasta n=6 y les pides a los alumnos que tanteen los casos n=7 u n=8).

Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

En teoría, basta medir 293 metabolitos para conocer el estado de los 2763 de una célula humana

El metaboloma humano (H. sapiens) comprende 5.283 reacciones bioquímicas que relacionan 2.763 metabolitos con una red metabólica de 21.026 conexiones. Para reconstruir el estado completo de esta red metabólica, es decir, la concentración de todos los metabolitos, ¿cuántas concentraciones de metabolitos hay que medir en laboratorio? La respuesta es 293 (para S. cerevisiae bastan 99 y para E. coli solo 96). ¿Sólo 293 permiten reconstruir el valor de 2.763? Así es, en teoría, claro, pues en la práctica que se pueda hacer no significa que sea factible lograrlo. Lo afirma un nuevo artículo interesantísimo de Albert-László Barabási y dos colegas que estudia la observabilidad (según la teoría del control) de redes metabólicas y de regulación génica. Todo biólogo matemático, o matemático biólogo, debería leer este artículo (tanto si trabaja con datos in silico como, y sobre todo, in vivo). El artículo técnico es Yang-Yu Liu, Jean-Jacques Slotine, Albert-László Barabási, «Observability of complex systems,» PNAS Early Edition, Jan 28, 2013. A los biólogos que tengan dificultades a la hora de entender el concepto de derivada de Lie y el jacobiano correspondiente les recomiendo consultar a cualquier matemático, o si no tienen ninguno a mano estudiar la tesis de licenciatura de Milena Anguelova, «Nonlinear Observability and Identiability: General Theory and a Case Study of a Kinetic Model for S. cerevisiae,» Department of Mathematics, Chalmers University of Technology and Göteborg University, April 2004 [pdf].

Matemáticas y morfogénesis de la ciudad como un ser vivo

La ciudad está «viva» ya que está siempre en movimiento, como un ser vivo nace, se desarrolla, se cura de sus lesiones (como daños de guerra) y, a veces, muere en parte o totalmente. Las ciudades presentan una amplia diversidad tanto en su forma general (circular, en expansión, lineal o incluso fractal) como en el aspecto de su sistema de calles (regular, orgánico o árboreo). Esta diversidad responde a limitaciones internas y externas y puede ser explicada por la matemática que modela el desarrollo de los seres vivos y los mecanismos de formación de patrones mediante morfogénesis. El resolución de Euler del problema de los puentes de Königsberg gracias al uso de un grafo en el que las aristas son las calles y los vértices son sus intersecciones, ha llevado a Thomas Courtat, del Laboratorio de Materiales y Sistemas Complejos, CNRS, Universidad de París, y sus colegas a desarrollar un modelo de la ciudad basado en su red de calles que permite analizar, manipular y explicar la morfogénesis de las ciudades. Las calles se dividen en pequeños trozos elementales que contienen toda la información adicional necesaria para reconstruir el mapa completo de la ciudad (posición y tipo de edificios, parques, etc.). Las calles pueden crecer de forma dinámica en función de una serie de reglas que modelan el crecimiento orgánico de la ciudad. La política urbanística de la ciudad se modela mediante un campo potencial que describe el atractivo a la hora de crecer de cada punto del espacio disponible para hacerlo. En la simulación del crecimiento de la ciudad, una vez elegido el punto más atractivo en cada momento se le conecta con la red de calles ya existente y se hace crecer en un pequeño trozo dicha red de calles. Courtat y sus colegas han introducido varias métricas (medidas) que caracterizan la topología de primer y segundo orden, la anisotropía y el crecimiento de las calles que permiten determinar el campo potencial que guía el crecimiento de la ciudad. Estos potenciales permiten comparar cualitativa y cuantitativamente ciudades entre sí. El artículo técnico es Thomas Courtat, Catherine Gloaguen, Stephane Douady, «Mathematics and Morphogenesis of the City, A Geometrical approach,» ArXiv, 8 Oct 2010.