La noticia matemática de la semana ha sido la resolución del problema del subespacio invariante en espacios de Hilbert, una conjetura propuesta por John von Neumann en 1935, gracias al trabajo conjunto de Carl C. Cowen (Universidad de Indiana-Purdue, Indianapolis, EEUU) y Eva A. Gallardo Gutiérrez (Universidad Complutense, Madrid), esta última matemática española de 39 años. Los autores de la demostración, tras tres años de duro trabajo, han presentado este importante resultado en el último congreso de la Real Sociedad Matemática Española celebrado en Santiago de Compostela. El problema resuelto es uno de los más importantes del área de Análisis Funcional y Teoría de Operadores.
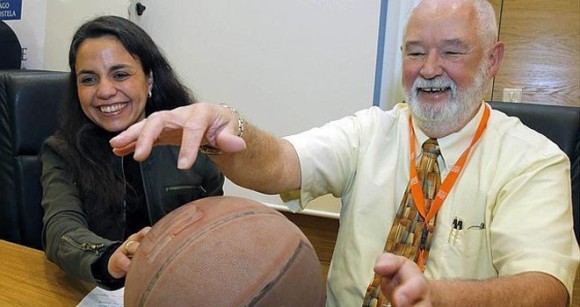
En la rueda de prensa, ambos matemáticos han ilustrado el problema utilizando un espacio de Hilbert de dimensión finita (un caso trivial): «Si pones a girar una pelota de baloncesto, siempre girará respecto a un eje determinado; este eje no varía en el giro y es el subespacio invariante asociado al operador lineal que representa el giro de la pelota.» Obviamente, este resultado en el espacio euclídeo es conocido desde el siglo XVIII. La versión en infinitas dimensiones no tiene aplicaciones tan fáciles de ilustrar, pero hay que recordar que los espacios de Hilbert son claves en física cuántica (como demostró John von Neumann hace 80 años) y que las aplicaciones de la física cuántica nos rodean por doquier.
Según los autores «hemos abordado el problema desde el punto de vista de la teoría de funciones de variable compleja, lo que da «cierta flexibilidad» a la hora de probar el resultado. (…) A veces uno piensa que ha cometido un error, pero la prueba la hemos revisado muchísimas veces, nos lo han revisado expertos en el área [que la recibieron el 10 de diciembre de 2012], y la sensación es que parece ser que de momento las cosas siguen en pie. La ventaja es que la solución es corta; no es un trabajo de trescientos folios con complicadas ideas, sino que son menos de veinte páginas. Las cuestiones cortas son sencillas de entender.» No puedo contar más detalles de la demostración (pues todavía no la he podido leer), por lo que me limitaré a enunciar el problema y hacer unos comentarios sobre su importancia.
Lo primero, la noticia en los medios: «Carl Cowen y Eva Gallardo presentan la solución afirmativa al «problema del subespacio invariante»,» Noticias RSME, ene 2013; Tamara Montero, «Presentan en la USC la resolución de un problema matemático de los años 30,» La Voz de Galicia, 25 ene 2013; «Resuelven uno de los problemas matemáticos más importantes del milenio,» ABC, 25 ene 2013.
Para una discusión técnica, centrada en los contraejemplos en espacios de Banach, recomiendo Carlos Domingo, «Problema del subespacio invariante,» Facultad de Matemáticas, Universitat de Barcelona, Curso 2010-2011; Joan Cerda, «Subespacios invariantes,» Departament de Matematica Aplicada i Analisi, Barcelona, abril 2012. En inglés están bien Terence Tao, «Finitary consequences of the invariant subspace problem,» What’s New, 29 Jun 2010; Adam Azzam, «The Invariant Subspace Problem and Lomonosov’s Theorem,» Part 1, Part 2, Part 3, 4-5 feb 2012.
PS: Una introducción muy buena al problema en B.S. Yadav, «The Invariant Subspace Problem,» Nieuw Archief voor Wiskunde 5: 148-152, Jun 2005, vía Christian Perfect, «The invariant subspace problem is solved for Hilbert spaces?,» The Aperiodical, Jan 26, 2013 (vía @gaussianos).
¿Qué es un espacio de Hilbert? Un espacio vectorial con un producto interior o escalar (que permite medir el ángulo entre dos vectores y definir el concepto de vectores ortogonales) que es completo (toda sucesión de Cauchy es convergente). Todo Hilbert es Banach. ¿Qué es un espacio de Banach? Un espacio vectorial con una norma (que permite calcular el módulo o tamaño de todo vector). Todo Banach es métrico. ¿Qué es un espacio métrico? Un espacio vectorial con una distancia (que permite medir la «distancia» entre cada par de vectores). ¿Qué es un espacio vectorial? Un espacio de objetos llamados vectores que se pueden sumar y que se pueden multiplicar por un escalar (número real o complejo). Todo espacio vectorial tiene una base (resultado del axioma de elección) y la dimensión del espacio vectorial es el cardinal de una cualquiera de sus bases.
Una aplicación lineal es una «función» entre dos espacios vectoriales que preserva las operaciones de suma y producto por escalar. En espacios vectoriales de dimensión finita las aplicaciones lineales se representan mediante matrices. Por el teorema fundamental del álgebra, toda matriz tiene autovalores. Asociado a cada autovalor hay uno o varios autovectores. La multiplicación de la matriz por dichos autovectores es aquivalente a multiplicar por el autovalor. Asociado a cada autovalor hay un subespacio vectorial llamado autoespacio. Este subespacio es invariante, pues la aplicación lineal (o matriz) aplicada a los vectores de dicho subespacio resulta en un vector dentro del mismo.
Las aplicaciones lineales también se llaman operadores lineales. En un espacio de Banach, se dice que un operador lineal es acotado si aplicado a todos los vectores del espacio el resultado tiene una norma acotada por una constante que solo depende del operador. Un operador lineal es compacto si aplicado a toda sucesión de vectores acotados, hay una subsucesión convergente. Todo operador lineal acotado tiene norma (es decir, se puede extender el concepto de norma de un vector al concepto de norma de un operador lineal acotado).
El espacio euclídeo de las transformaciones de objetos tridimensionales que preservan la forma de los objetos es un espacio de Hilbert de dimensión finita. Todo operador lineal en dicho espacio corresponde a un matriz y por tanto tiene un subespacio invariante. De ahí que al rotar la pelota de baloncesto siempre rote alrededor de algún eje. En un espacio de Hilbert H de dimensión infinita el asunto es más complicado.
El problema del subespacio invariante plantea la siguiente cuestión: Si H es un espacio de Hilbert, ¿es cierto que para todo operador lineal y acotado T ∈ L(H), existe siempre algún subespacio G ⊂ H cerrado que es T-invariante, T(G) ⊂ G, sin ser trivial? Repito, para un espacio H de dimensión finita el resultado es trivial, siempre existen subespacios invariantes; los autovalores de T (que será una matriz) tienen asociados subespacios propios (autoespacios en cuya base están los autovectores) que son invariantes. Esta cuestión en dimensión infinita no parece muy complicada, pero se ha resistido durante casi 80 años al esfuerzo de muchos matemáticos.
En 1935, John von Neumann probó que todo operador compacto en un espacio de Hilbert tiene subespacios invariantes no triviales, hecho que fue generalizado a espacios de Banach en 1954 por N. Aronszajn y K.T. Smith. P. Enflo en 1976 y C. Read en 1985 encontraron ejemplos de operadores lineales acotados que carecían de subespacios invariantes no triviales en espacios de Banach (recuerda que todo Hilbert es Banach, pero no al contrario). Todos los contraejemplos conocidos son sobre espacios de Banach no reflexivos (un Banach B es reflexivo si la aplicación «natural» entre B y B** (el dual del dual de B) es un isomorfismo de espacios de Banach); el Teorema Pequeño de Riesz garantiza que todo espacio de Hilbert es reflexivo.
Hasta que no tenga acceso a la nueva demostración no podré ofrecer más información.
Coda final: Esta entrada participa en la Edición 3.1415926535 del Carnaval de Matemáticas organizado por el blog «La Aventura de la Ciencia» del físico Daniel Martín Reina (Sevilla, España). Mañana es el último día para las contribuciones al Carnaval de Matemáticas, ¡anímate, aún estás a tiempo!

Para los que no entendemos mucho del tema, lo realmente Im-Presionante (en dos palabras), es que se pueda resolver un mproblema tan intrincado, con un océano por medio.
Enhorabuena a los dos, y a la Real Sociedad Matemática Española, que se ha dado el gustazo de exponerlo, como aquel que dice, en campo propio.
No ha habido océano de por medio. Creo que fue producto del año sabático que Carl Cowen pasó invitado en la Complutense de Madrid.
Por cierto, que ahora mismo, el preprint en cuestión es el objeto matemático más codiciado. Nadie que yo conozca y haya preguntado lo tiene.
Seria bueno tener el preprint para echarle un vistazo.
Una buena y muy clarificadora explicación.
Mientras leía esa secuencia «Todo A es B ¿Que es B?, … » estaba escuchando una musica rock-rapida, y pegaba de letra:)
Yo no tengo acceso al preprint todavía, pero creo que la solución se basa en una reducción de G.-C. Rota [On models for linear operators, Comm. Pure Appl. Math. 13 (1960), 469-472]: basta probar que los subespecies invariantes minimales de una backward shift de multiplicidad infinita son siempre de dimensión finita.
Vaya realmente es un resultado bellísimo (imagino que potencialmente tendrá muchas importantes aplicaciones en mecánica cuántica), Me sorprendió la noticia por que no tenía idea que fuera una cuestión abierta aparentemente cualquiera podría pensar que es algo trivial pero bueno los espacios normados de dimensión infinita guardan esta clase de asombrosas sorpresas, por ejemplo creo recordar que alguna vez el maestro de Análisis funcional mencionó que en los espacios de sucesiones reales equipados con la norma p no se sabe cuales son los compactos no triviales, una pregunta que parecería básica. También recuerdo (con todo el respeto del mundo lo digo y sin afán de ofender a nadie) que decía que gran parte de física teórica se podía entender completamente en términos de ser una rama del análisis funcional justamente (no afirmo que así sea) pero lo recordé por que alguien en este blog una vez mencionó que había una serie de libros en donde mostraban a la física teórica desde el punto de vista del análisis funcional durante una excelente entrada de Francis sobre la estabilidad de materia, supongo que debe ser muy interesante.